www.HAGMOLEN.nl
Het werk "Over Drijvende Lichamen" van Archimedes
G. Hagmolen of ten Have & M. Topper
Inleiding
Heb je je wel eens afgevraagd waarom je bad-eend drijft? En waarom ie niet
koppie onder gaat?
Al in de derde eeuw voor Christus hield iemand zich bezig met de vraag
wanneer een voorwerp blijft drijven. En zo ja, in welke stand het blijft
drijven: rechtop, plat, scheef... Die iemand, Archimedes, publiceerde zijn
ontdekkingen in het werk Over drijvende lichamen, bestaande uit twee
boeken. Het eerste boek bestaat uit negen proposities (stellingen), waarvan de
eerste zeven gaan over wanneer een lichaam drijft, hoe diep het in het water
zakt en over de "Wet van Archimedes". De laatste twee proposities van
het eerste boek en de tien van het tweede boek gaan over evenwichtsstanden van
twee verschillende ruimtelijke figuren. Voordat we de belangrijkste proposities
langslopen, geven we eerst een overzicht van de manier waarop dit werk
overgeleverd is.
Tot slot willen we Henk Bos, Jan Hogendijk en de overige deelnemers van het
seminarium Archimedes, gehouden in het voorjaar van 2000 bij de faculteit
Wiskunde aan de Universiteit Utrecht, bedanken voor de inspiratie die we nodig
hadden om dit werk van Archimedes op een leuke manier voor het voetlicht te
brengen.
Gerbrand Hagmolen of ten Have
Mario Topper
De overlevering
In de negende eeuw werd door Leoon van Thessalonika een manuscript
samengesteld met werken van Archimedes. Heiberg noemt dit manuscript codex A.
Over drijvende lichamen komt er niet in voor. Het origineel is tussen 1550
en 1564 verloren gegaan. Verder was er een verzameling van werken op het gebied
van mechanica en optica, die Heiberg codex B
noemt. Dit manuscript was in 1295 en 1311 in de pauselijke bibliotheek. Daarna
is het spoorloos.
In 1269:
Een groot deel van codex A werd door de dominicaan Willem van Moerbeke in het
Latijn vertaald. Van 1268 tot 1280 werkte hij aan het pauselijk hof om
verschillende Griekse teksten toegankelijk te maken door ze te vertalen. Het
oorspronkelijke handschrift werd in 1884 in Rome teruggevonden: de codex B van
Heiberg. De tekst van Moerbeke bevat één werk van Archimedes dat niet in codex
A voorkomt, namelijk Over drijvende lichamen. Hij moet dus nog een andere
bron gebruikt hebben: codex B.
In de 16e eeuw:
De eerste gedrukte uitgaven van werken van Archimedes kwamen tot stand. De
oudste hiervan kwam voor in een boekje van de wiskundige Luca Gauricio uit
Napels, over de Kwadratuur van de cirkel. Dit verscheen in 1503 in
Venetië. Hierin staat de Latijnse vertaling van Cirkelmeting en Kwadratuur
van de parabool, ontleend aan codex B.
In 1543:
Een letterlijke kopie van de bovenstaande editie werd door Nicolo Tartaglia
gepubliceerd. Hij voegde er de Latijnse vertaling van Evenwichten van vlakke
figuren en Over drijvende lichamen aan toe. Volgens Heiberg heeft hij
de uitgave van Gauricio en een afschrift van codex B met fouten en al
overschreven.
In 1565:
In Venetië verscheen in 1558 een Latijnse vertaling van een aantal werken van
Archimedes verzorgd door Federigo Commandino. De tekst is afkomstig uit codex B
of een afschrift daarvan. In 1565 voegde hij er een vertaling van het werk Over
drijvende lichamen aan toe.
In 1828:
Al die tijd ontbrak de Griekse tekst van Over drijvende lichamen. De
kardinaal Angelus Maii publiceerde op grond van twee in het Vaticaan ontdekte
handschriften een aantal Griekse fragmenten van boek I. Later bleken deze
teksten terugvertaald te zijn vanuit het Latijn naar het Grieks, niet eerder dan
in de zestiende eeuw.
In 1899:
Een nieuw Archimedes-handschrift werd ontdekt, doordat de aandacht van Heiberg
viel op een bericht van Papadopoulos Kerameus over een palimpsest met een
oorsronkelijk wiskundige inhoud in de bibliotheek van het klooster S. Sepulchri
in Jeruzalem.
In 1906-1908:
Heiberg onderzocht dit manuscript, de codex C, in Constantinopel. Het bleek een
op perkament geschreven Archimedes-tekst uit de tiende eeuw te bevatten. Heiberg
ontcijferde de oorspronkelijke tekst en vond naast een onbekend werk van
Archimedes, de Methode, een aanzienlijk deel van de Griekse tekst van Over
drijvende lichamen.
De in codex C nieuw gevonden teksten komen nog niet voor in de Engelse
uitgave van Heath uit 1897. Heath gebruikte de uitgaven van Tartaglia en
Commandino. Later is de Methode er wel aan toegevoegd, maar Over
drijvende lichamen is niet herzien in deze uitgave. Dit verklaart, waarom
bepaalde bewijzen in de uitgave van Heath niet of onvolledig opgenomen zijn. De
vertaling van Paul Ver Eecke gebruikt de teksten uit codex C wel.
Het eerste postulaat
Boek I begint met een postulaat over de aard van vloeistoffen. Wat Archimedes
met dit postulaat bedoelt, wordt pas duidelijk in de bewijzen van de eerste
proposities. Hieronder het postulaat, in de vertaling van Dijksterhuis.

"Laat ondersteld worden, dat de vloeistof van zodanige aard is, dat van
haar op hetzelfde niveau liggende en aan elkaar grenzende delen het minder sterk
gedrukte wordt weggestoten door het sterker gedrukte en dat elk van haar delen
wordt gedrukt door de vloeistof die er recht boven ligt, indien de vloeistof
niet ergens in is opgesloten en niet door iets anders gedrukt wordt."
De verschijnselen in de proposities spelen zich op aarde af, maar de aarde
zèlf is weggedacht. Alleen het middelpunt ervan is nog over. Om dat middelpunt
hoopt het water zich op. Archimedes gebruikt hier het wereldbeeld van
Aristoteles. Volgens Aristoteles heeft elk van de vier elementen water, aarde,
lucht en vuur een neiging om zijn natuurlijke plaats op te zoeken. Vuur heeft
van nature een opwaartse neiging. Zijn plaats ligt tussen lucht en het hemelse
element ether in. Aarde is zwaar, heeft een neerwaartse neiging die het
middelpunt van de wereld. Water en lucht zitten hier tussenin: water boven aarde
en onder lucht, lucht tussen vuur en water. De elementen zoeken zo hun
natuurlijke plaats in de kosmos. Daarnaast zoeken ze ook hun natuurlijke
toestand, namelijk rust.
De verticalen waarlangs het streven omlaag gericht is, komen samen in een
punt, namelijk in het middelpunt van de aarde. In andere werken van Archimedes,
zoals in de Methode, zijn ze parallel. In boek II van Over drijvende lichamen
zijn ze ook evenwijdig.
In de Engelse bewerking van Heath klopt de tekst van het postulaat niet. Het
laatste gedeelte luidt bij hem namelijk als volgt: "... indien de
vloeistof ergens in is opgesloten en door iets anders gedrukt wordt."
in plaats van "... indien de vloeistof niet ergens in is
opgesloten en niet door iets anders gedrukt wordt.". Het
verschil is te verklaren uit het feit dat Heath voor zijn bewerking nog niet de
beschikking had over de Griekse tekst (in codex C).
De eerste 7 proposities van boek I
De eerste propositie die volgt op postulaat 1 zegt dat een oppervlak, dat
door alle platte vlakken, die een bepaald punt bevatten, gesneden wordt volgens
cirkels, die dat punt tot centrum hebben, een bol is. Archimedes bewijst dit
eenvoudig uit het ongerijmde (zie vertaling van T.L. Heath). Dit resultaat
gebruikt Archimedes voor propositie 2. Omdat deze propositie interessant genoeg
is én we er later op terugkomen zullen we deze volledig behandelen.
Propositie 2
Het oppervlak van iedere vloeistof in rust is een boloppervlak met het
middelpunt gelijk aan het middelpunt van de aardbol.
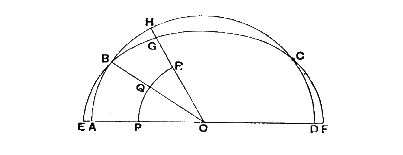
De figuur stelt een doorsnede voor met een plat vlak door het middelpunt
O van de aarde, dat het vloeistofoppervlak snijdt volgens ABCD. Nu is ABCD
dus een cirkel. Stel dat dit niet zo is, dan is er een paar lijnen van O
naar ABCD die niet gelijk zijn. Trek een cirkel EBGF om O met OB als straal
en zo dat
pEOB =
pBOH en trek een
cirkel PQR om O met straal OP < OB.
Nu geldt PQ = QR. PQ wordt gedrukt door de vloeistof in ABQP, terwijl QR
gedrukt wordt door de vloeistof in BGRQ. Blijkbaar is de laatste hoeveelheid
groter dan de eerste, zodat volgens het postulaat de vloeistof niet in rust
kan zijn. Is de vloeistof wel in rust, dan moet ABCD een cirkel zijn met
middelpunt O. Omdat het snijvlak door O willekeurig is, volgt hieruit
volgens propositie 1 dat het oppervlak van vloeistof in rust een
boloppervlak is, waarvan het middelpunt samenvalt met het middelpunt van de
aarde.
Hierna volgen twee "kwalitatieve" proposities (3 en 4), die gevolgd
wordt door een "kwantitatieve" propositie (5) over ruimtelijke
lichamen geworpen in vloeistof.
Propositie 3 zegt dat een ruimtelijk lichaam dat evenzwaar is als de
vloeistof - daar wordt mee bedoeld dat ze dezelfde soortelijke massa hebben - zo
ver in de vloeistof zakt dat de oppervlakken van het lichaam niet meer uitsteken
boven dat van de vloeistof en het lichaam niet verder naar beneden zakt.
Propositie 4 zegt dat een ruimtelijk lichaam, met een kleinere soortelijke
massa dan de vloeistof, niet geheel in de vloeistof zal zakken, maar ten dele
boven het vloeistofoppervlak uit zal steken.
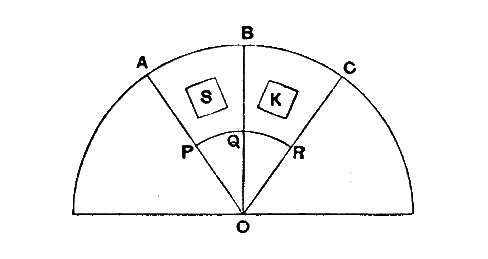
Het bewijs van beiden berust op het volgende. We nemen twee aangrenzende
piramides met als grondvlak het vloeistofoppervlak (ABC) en als top het
middelpunt van de aarde (O). Dichter bij O nemen we een ander boloppervlak (PQR).
In de ene piramide "werpen" we het ruimtelijke lichaam (S), in het
andere aanschouwen we een congruent "blokje" vloeistof (K). Vervolgens
vergelijken we in de ene piramide de druk op PQR met de druk op PQR in de andere
piramide. Als die ongelijk zijn, dan kan de vloeistof niet in rust zijn, aldus
het postulaat, en zal S stijgen of dalen zodat de vloeistof wel in rust komt te
staan.
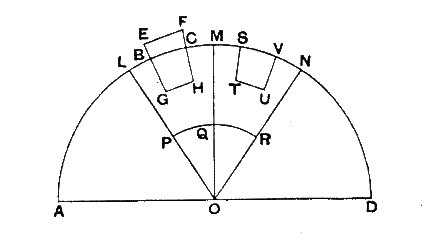
In propositie 4 wordt gezegd dat er een deel van het lichaam boven de
vloeistof uitsteekt, of beter gezegd er maar een deel in de vloeistof zakt,
terwijl propositie 5 precies aangeeft hoeveel het lichaam in de vloeistof zakt.
Propositie 5 zegt namelijk dat een ruimtelijk lichaam, dat een kleinere
soortelijke massa heeft dan de vloeistof, zover in de vloeistof zakt, dat een
"blokje" vloeistof, dat hetzelfde volume heeft als het ondergedompelde
deel van het lichaam, evenveel zwaarte heeft als het hele lichaam. Het bewijs is
heel eenvoudig. In de onderstaande figuur is EFGH het gegeven lichaam en STUV
het "blokje" vloeistof (congruent met BCGH, het ondergedompelde deel).
Omdat de vloeistof in rust is, moet de zwaarte van EFGH gelijk zijn aan die van
STUV.
We hebben nu gekeken naar ruimtelijke lichamen geworpen in vloeistof en
gekeken naar hun rust-situatie. Archimedes gaat nog een stapje verder; hij geeft
in propositie 6 weer wat de kracht is waarmee een naar beneden gedwongen
lichaam, lichter dan de vloeistof, weer omhoog gedreven wordt. Deze kracht is
gelijk aan het verschil in zwaarte tussen het lichaam en een "blokje"
vloeistof dat even groot is als het lichaam. Het bewijs is anders als de
eerdere, maar vergelijkbaar met die van de hierna genoemde propositie. Omdat die
propositie (de "Wet van Archimedes") erg bekend en belangrijk is,
zullen we die volledig doornemen.
Propositie 7
Lichamen, zwaarder dan de vloeistof, in de vloeistof geworpen, zullen
omlaag worden gevoerd, zover ze kunnen dalen en ze zullen in de vloeistof
zoveel lichter zijn als een deel van de vloeistof, van hetzelfde volume als
het lichaam, zwaarte heeft.
In de "Grote Winkler Prins" 7e druk staat de "Wet
van Archimedes" als volgt: Een lichaam, dat geheel of gedeeltelijk in een
vloeistof is gedompeld, ondervindt een opwaartse kracht waardoor zijn gewicht
(schijnbaar) evenveel vermindert als de verplaatste vloeistof weegt.
DEMO-IDEE:
Maak van K’NEX (of Mecano, Temsi)
een balans, neem twee gelijke gewichten en hang deze aan weerszijde van de
balans. Laat nu één gewicht in een bak met water zakken (bijvoorbeeld door het
optillen van de waterbak). De balans slaat uit naar de kant van het
"droge" gewicht.

Het eerste deel van de propositie is makkelijk te bewijzen op de manier zoals
besproken is bij propositie 3 en 4. Het tweede is interessanter.
Zij A het gegeven lichaam met gewicht G+H, terwijl een evengroot volume
vloeistof G weegt. Neem een lichaam B met gewicht G, zodat een evengroot
volume vloeistof een gewicht G+H heeft.

Verenig nu A en B tot één lichaam met gewicht 2G+H. Een even groot
volume vloeistof weegt ook 2G+H. A en B zullen dus samen zweven; B alleen
zou volgens propositie 6 omhoog worden gedreven met een kracht, gelijk aan
H. H stelt dus ook de kracht voor, waarmee A alleen omlaag zou worden
gevoerd, dus het gewicht van A in de vloeistof. A is dus in de vloeistof een
bedrag G lichter dan daar buiten.
Bij deze propositie hoort de bekende legende die verteld dat Archimedes de
zuiverheid van de gouden wijkrans van koning Hieron moest onderzoeken, dat hij,
over deze opgave peinzend, ging baden, en daardoor ineens op het idee komt, hoe
hij het volume kan bepalen (hetzij door weging van het overlopende water bij
onderdompeling in een vat, zoals Vitruvius meent, of volgens anderen door meting
van de opwaartse druk) en hoe hij dan, "Heureka, heureka!" roepend,
naakt naar huis rent.

De Kroon
Met behulp van propositie 7 kan je als volgt de verhouding tussen het goud en
het zilver onderzoeken. Laat G het gewicht zijn van de kroon, gg
en gz respectievelijk het gewicht van het goud en het zilver
in de kroon, zo dat G = gg + gz .
(1) Neem een gewicht gelijk aan G van puur goud en weeg het buiten en
in de vloeistof. Laat Fg het gewichtsverschil zijn. Er volgt
dan dat het gewichtsverlies van gg gelijk is aan
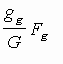 .
.
(2) Neem een gewicht gelijk aan G van puur zilver en weeg het buiten
en in de vloeistof. Laat Fz het gewichtsverschil zijn. Er
volgt dan dat het gewichtsverlies van gz gelijk is aan 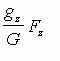 .
.
(3) Weeg tot slot de kroon zelf in de vloeistof en laat F
het gewichtsverlies zijn.
We hebben dan 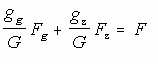 , en dat
is gelijk aan ggFg
+ gzFz = (gg+gz)F,
en dus
, en dat
is gelijk aan ggFg
+ gzFz = (gg+gz)F,
en dus 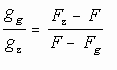 .
.
Volgens de auteur van het gedicht "de ponderibus et
mensuris", waarschijnlijk geschreven rond 500 (na
Chr.), heeft Archimedes een methode als deze gebruikt. Echter Vitruvius schreef
hem toe dat hij het volume bepaalde van de lichamen. Volgens Vitruvius heeft
Archimedes namelijk het volume bepaald van de kroon, van puur goud met hetzelfde
gewicht en van puur zilver met hetzelfde gewicht. Dit ligt eigenlijk ook meer
voor de hand als je de legende moet geloven: hij stapt in een vol bad en ontdekt
dat er door het in bad stappen water over de rand stroomt, maar hoeveel?
Voor deze oplosmethode geldt bovenstaande redenering, maar nu met volume V,
Vg en Vz in plaats van gewichtsverlies F,
Fg en Fz. De laatste vergelijking wordt dan 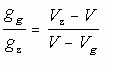 .
Merk op dat deze (natuurlijk) gelijk aan elkaar zijn.
.
Merk op dat deze (natuurlijk) gelijk aan elkaar zijn.
DISCUSSIE:
Volgens de vertalingen gebruikt
Archimedes in zijn teksten de volgende termen: druk (eenheid nu: Nm-2),
kracht (eenheid nu: N) en gewicht (eenheid nu: N). Druk werkt bij hem van boven
naar beneden op een lichaam, kracht van beneden naar boven en beide worden ze
uitgedrukt in gewicht. Zou Archimedes al echt een krachtbegrip hebben gehad? En
hoe zit dat dan met druk?
Waarschijnlijk zal Archimedes wel iets van een krachtbegrip hebben gehad,
maar dat moet je niet zien in het licht van het moderne krachtbegrip. In zijn
geval is druk net zo iets als kracht, waardoor de ongelijkheid in het moderne
geval wegvalt.
De laatste 2 proposities van boek I
Deze twee proposities gaan over de evenwichtstand van een willekeurig
drijvend bolsegment in vloeistof.
DEMO-IDEE:
Neem een bak met water en een houten
bol(-letje). Zaag of schuur een deel van de bol af, zodat je een bolsegment over
houdt. Zet het bolsegment schuin in water, maar zo dat de basis volledig boven
de waterspiegel is. Bij loslaten zal het bolsegment draaien tot de
evenwichtstand met verticale as. Doe hetzelfde met de basis volledig onder de
waterspiegel.
Propositie 8
Als een lichaam in de vorm van een bolsegment, en van een kleiner
soortelijk gewicht dan de vloeistof, in de vloeistof wordt gelaten en wel zo
dat zijn basis niet het vloeistofoppervlak raakt, dan zal het lichaam rusten
in zo’n positie dat zijn as loodrecht staat op het vloeistofoppervlak.
Wordt het lichaam uit z’n ruststand gehaald zodat zijn basis aan één
kant het vloeistofoppervlak raakt en daarna losgelaten, dan zal het niet zo
blijven staan, maar terugkeren naar zijn symmetrische positie.
Propositie 9
Als een lichaam in de vorm van een bolsegment, en van een kleiner
soortelijk gewicht dan de vloeistof, in de vloeistof wordt gelaten en wel zo
dat zijn basis geheel onder het vloeistofoppervlak valt, dan zal het lichaam
rusten in zo’n positie dat zijn as loodrecht staan op het
vloeistofoppervlak.
Archimedes kon het zwaartepunt van een bolsegment bepalen (de Methode:
propositie 5). Zo heb je in een drijvend bolsegment het middelpunt van de bol
(O), het zwaartepunt van het hele segment (C), het zwaartepunt van het
bolsegment onder de vloeistof (F), deze ligt recht onder O (ga na!), en het
zwaartepunt van het deel boven de vloeistof (H). Logischerwijs liggen F, C en H
op één lijn. Stel dat deze lijn niet verticaal staat, maar schuin. Dan ligt H
aan een kant van de verticaal door C en F aan de andere kant. Stel H ligt
rechts. Dan drukt H naar beneden en F omhoog, zodat het segment draait, waardoor
H naar links verschuift en F naar rechts totdat de lijn door F, C en H verticaal
staat. Nu wordt de kracht waarmee H naar beneden wil opgeheven door de kracht
waarmee F naar boven wil. De evenwichtstand is bereikt.
In principe is het voldoende om naar C en F te kijken. Dit is wat Archimedes
ook gedaan zal hebben, want dan heb je alleen zwaartepunten van bolsegmenten
nodig. Het zwaartepunt H vinden is niet zo eenvoudig namelijk en de vraag is of
Archimedes dat wel kon.
DEMO-IDEE:
Maak van stevig karton een grote
bolsegment-doorsnede, het bolsegment-model. Maak een klein ophanggaatje in het
middelpunt van de cirkel (O) waaruit de doorsnede is gemaakt. Bepaal het
zwaartepunt van de doorsnede bijvoorbeeld door het op je vinger te balanceren en
geef dit punt aan op het model. Plak met plakband een paperclip omgebogen tot
haakje op een bordmagneet en hang hier het model in O aan op. Neem een dun
touwtje en maak een lusje aan een uiteinde. Rijg het touwtje twee maal door een
kraal, zodat de kraal in een lus gevangen wordt en verzwaar met bijvoorbeeld een
moertje het andere uiteinde van het touwtje. Hang dit touwtje aan het haakje
voor het model. De kraal stelt nu het zwaartepunt F voor en is in hoogte
stelbaar. Neem een tweede, wat dikker touwtje, met een sterk afwijkende kleur
van het model. Span dit touwtje met twee bordmagneten horizontaal over het
model; dit stelt de waterspiegel voor. Eventueel is nog een punt H te maken van
een nippeltje die opgehangen wordt aan een touwtje en een bordmagneet. Het
geheel is nu een duidelijk (draaibaar) demonstratie-model van hetgeen hier boven
als bewijsidee gegeven is.

DISCUSSIE: Je zou je kunnen afvragen hoe het bolsegment draait: over
welk punt? Is het wel een punt? Dit is echter een erg lastige en vervelende
vraag, waar we nu niet op in gaan. Bovendien heeft Archimedes het ook niet over
beweging.
De proposities van boek II
INTERMEZZO
Boek II gaat over rechte segmenten van
paraboloïden. Een paraboloïde ontstaat wanneer een parabool om zijn as
gedraaid wordt: het is een omwentelingslichaam. Een segment van een paraboloïde
ontstaat door een paraboloïde te snijden met een plat vlak. Als dit vlak
loodrecht op de omwentelingsas staat, dan is het segment recht.
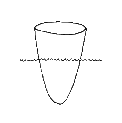
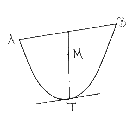
De as van een segment valt niet altijd samen met de omwentelingsas van de
paraboloïde. Kijk naar de doorsnede van een segment van een paraboloïde
hierboven. Trek de raaklijn aan de parabool evenwijdig aan de basis AB. Deze
raakt de parabool in een punt T. Dit is de top van het segment. Laat C het
midden zijn van de basis AB. Dan is CT de as van het segment. Deze valt samen
met de omwentelingsas in het geval van een recht segment. Archimedes heeft in de
Methode het zwaartepunt van een segment van een paraboloïde bepaald. Dit
zwaartepunt ligt op de as van het segment, op
b
van de top.
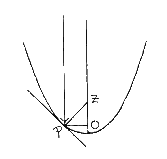
Elke parabool heeft een parameter. deze is voor ons snel zichtbaar als we
coördinaten kiezen en een vergelijking voor de parabool opstellen: x2
= py. Archimedes gebruikt deze parameter bij gevalsonderscheidingen. Hij komt op
de volgende manier naar voren. Laat ZO de as van de parabool zijn. De lijn door
P is een raaklijn aan de parabool. De loodlijn vanuit P treft de as in Z. Trek
verder OP loodrecht op de as. Dan is ZO = ½p. Dit is dus onafhankelijk van de
ligging van het punt P op de parabool.
Archimedes is in het tweede boek over drijvende lichamen op
zoek naar "the positions of rest" oftewel evenwichtsstanden van rechte
segmenten van paraboloïden. Hij onderzoekt negen gevallen: vijf waarbij de
basis boven het vloeistofoppervlak is en vier met de basis onder het oppervlak.
Om de gevallen te onderscheiden, maakt Archimedes gebruik van
twee "basis-kenmerken" van elke paraboloïde. Dat zijn:
Deze twee factoren staan niet los van elkaar, en dat is in
hele boek goed te merken.
Heel informeel is de gedachtegang als volgt. Heb je een heel plat segment van
een paraboloïde, dan kun je je goed voorstellen dat het segment rechtop gaat
staan. Zou je hetzelfde segment hoger maken, dan komt er een punt dat het gaat
kapseizen. Maak je ditzelfde hoge segment echter van zwaarder materiaal, dan
komt het dieper in de vloeistof te liggen en zou het daardoor weer rechtop
kunnen gaan staan: de vloeistof kan een stabiliserende rol spelen.
DEMO-IDEE:
Maak van papier
kleine paraboloïde-doorsneden met verschillende verhoudingen tussen breedte en
hoogte. Teken op een sheet een horizontale lijn, de waterspiegel. Discussieer
met de doorsneden of het een verticaal evenwichtstand heeft of dat het om zal
klappen. Varieer hierin ook de diepteligging van de paraboloïde. (Zie ook de
plaatjes bij de proposities 2, 4, 6, 8 en 10).
Uiteraard geldt in de volgende proposities dat het
paraboloïdesegment een kleiner soortelijk gewicht heeft dan de vloeistof waarin
het geplaatst wordt. Voor de overzichtelijkheid is deze eis soms weggelaten.
We zullen hier en daar de afkortingen sgs voor soortelijk
gewicht segment en sgv voor soortelijk gewicht vloeistof
gebruiken.
Propositie 2 is de eerste propositie over de paraboloïde. De dichtheid
speelt hierin nog geen rol.
Propositie 2
Wanneer een recht segment van een paraboloïde een as heeft die niet
groter is dan ¾p (met p de parameter van de genererende parabool; py=x2),
dan zal het, zo in de vloeistof geplaatst dat zijn basis het
vloeistofoppervlak niet raakt, als het hellend geplaatst wordt, niet hellend
blijven, maar zich rechtop plaatsen.

Dus een recht segment van een paraboloïde, waarvoor geldt dat as
#
¾p, gaat rechtop staan. Archimedes gaat van deze voorwaarde uit en bewijst
daarmee de propositie. interessanter is het om na te gaan hoe Archimedes aan
deze voorwaarde gekomen kan zijn.
Het idee is als volgt. Een vrij plat segment gaat zeker rechtop staan in de
vloeistof. Hoe hoger het segment is, hoe groter de kans wordt dat het gaat
kapseizen. Je kunt je afvragen hoe hoog een segment kan zijn zo dat het nog net
rechtop blijft staan.
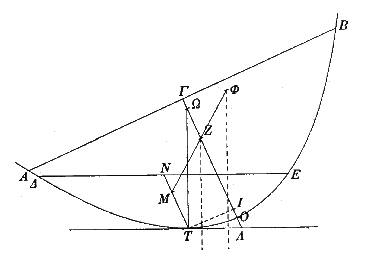
In de figuur hierboven is een doorsnede van een paraboloïde_segment te zien.
Het snijvlak gaat door het zwaartepunt van het segment en staat loodrecht op het
vloeistofoppervlak. Hierin zijn getekend:
- de as van het segment, met daarop het zwaartepunt Z van het hele segment
- de raaklijn aan de parabool, evenwijdig aan het vloeistofoppervlak
- de as van het ondergedompelde deel, met daarop het zwaartepunt M van dit
deel
- de lijn door M en Z, met daarop ook het zwaartepunt
M
van het deel van de paraboloïde dat boven de vloeistof uitsteekt
Om ervoor te zorgen dat het segment rechtop gaat staan (zodat de bovenkant
evenwijdig is aan het vloeistofoppervlak) moet het zwaartepunt M van het
ondergedompelde deel links van het zwaartepunt Z van het hele segment liggen. In
de figuur komt dit overeen met O
S
> OZ oftewel OS
> b
as.
Merk op dat IS
< OS, dus
een voldoende voorwaarde hiervoor is IS
$ OZ.
Omdat IS =
½p kan dit worden herschreven tot ½p $
b as
oftewel as # ¾p.
Is de waarde ¾p als maximale lengte voor de as eenmaal gevonden, dan ligt een
bewijs voor de propositie heel erg voor de hand: as #
¾p 6 ½p $
b as 6
IS $
OZ 6 OS
> OZ.
Dit betekent dat M links van de verticaal door Z ligt.
Een paraboloïde die hoger is dan ¾p zou dus kunnen kapseizen. Maar wordt zo’n
segment van een soortelijk zwaarder materiaal gemaakt, dan zakt het dieper de
vloeistof in en kan het daardoor (misschien) wel rechtop staan. de dichtheid van
het segment ten opzicht van de dichtheid van de vloeistof bepaalt hoe ver het
segment in de vloeistof zakt. In propositie 4 onderzoekt Archimedes hoe zwaar
een paraboloïde_segment met een as langer dan ¾p moet zijn om een
evenwichtsstand te hebben waarbij de as verticaal staat.
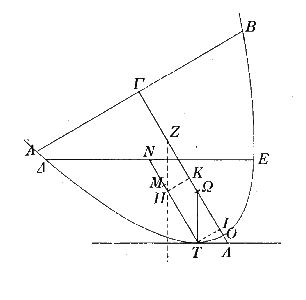
Om het segment zo te laten kantelen dat de as verticaal gaat staan, is het
ook hier nodig dat het zwaartepunt M van het ondergedompelde deel links van de
verticaal door Z ligt. Door dit uit te werken kan de extra voorwaarde uit
propositie 4 gevonden worden, namelijk dat (sgs) : (sgv) niet kleiner mag zijn
dan (lengte as - ¾p)2 : (lengte as)2.
Propositie 4
Wanneer een recht segment van een paraboloïde een
as heeft die groter is dan ¾p en er geldt dat (soortelijk gewicht segment)
: (soortelijk gewicht vloeistof) niet kleiner is dan (lengte as - ¾p)2
: (lengte as)2, dan zal het, zo in de vloeistof geplaatst dat
zijn basis het vloeistofoppervlak niet raakt, als het hellend geplaatst
wordt, niet hellend blijven, maar zich rechtop plaatsen.

Archimedes gaat verder met het geval dat de basis nog boven het water
uitsteekt, maar waarbij de rand van de basis het water net raakt. Hij
veronderstelt ¾p < as < 15/8p en laat zien dat de
paraboloïde niet in deze positie kan blijven staan. Er is een kracht die de
parabool meer rechtop duwt. Dit laat de mogelijkheid van een stabiel evenwicht
open.
Propositie 6
Wanneer een recht segment van een paraboloïde een as heeft die groter
is dan ¾p en kleiner is dan 15/8p, dan zal het, zo
in de vloeistof geplaatst dat zijn basis raakt aan het vloeistofoppervlak,
nooit in een positie blijven waarin de basis het vloeistofoppervlak
slechts in één punt raakt.

Waarom deze propositie? Archimedes heeft in zijn bewijzen nodig, dat het
deel van de paraboloïde onder het vloeistofoppervlak een segment van een
paraboloïde is. Dan kent hij namelijk de plaats van het zwaartepunt van het
ondergedompelde deel. Propositie 6 geeft de garantie dat de basis boven het
vloeistofoppervlak blijft, en dat het ondergedompelde deel dus een (scheef)
segment van een paraboloïde is. De factor 15/8 is
afkomstig van de eis dat er nog een "terugdrijvende" kracht moet
zijn.
Propositie 8 geeft nu dat deze paraboloïde blijft staan in een schuine
stand. Archimedes construeert in het bewijs ervan zelfs de exacte hoek.
Propositie 8
Gegeven een lichaam in de vorm van een recht segment van een
paraboloïde met een as die groter is dan ¾p en kleiner is dan 15/8p,
en met de eigenschap dat (soortelijk gewicht segment) : (soortelijk
gewicht vloeistof) kleiner is dan (lengte as - ¾p)2 : (lengte
as)2. Dit lichaam zal, als het hellend in de vloeistof wordt
geplaatst maar zo dat zijn basis het vloeistofoppervlak niet raakt, niet
in de stand blijven staan en zich ook niet rechtop plaatsen, behalve als
zijn as een hoek maakt met het vloeistofoppervlak die nader omschreven zal
worden.

Merk op dat nu alle mogelijke rechte segmenten van een paraboloïde met een
as < 15/8p behandeld zijn. Tot slot behandelt
Archimedes in propositie 10 het geval waarbij de as langer is dan 15/8p.
Binnen die ene propositie onderscheidt hij zes mogelijkheden. De
gevalsonderscheiding binnen de propositie voert hij uit op de verhouding
(soortelijk gewicht vloeistof) : (soortelijk gewicht segment). Deze verhouding
kan denkbeeldig gevarieerd worden door het soortelijk gewicht van de vloeistof
vast te laten en het soortelijk gewicht van het segment te variëren. Dit
gebeurt bijvoorbeeld als je segmenten van verschillende materialen uitprobeert
in een bak water. Een (relatief) zwaar segment zakt ver de vloeistof in, en
zijn basis zal evenwijdig aan het vloeistofoppervlak zijn (figuur I).
Hetzelfde segment, gemaakt van lichter materiaal, zakt minder ver de vloeistof
in en zal scheef gaan hangen (II). Wordt het segment opnieuw lichter, dan
hangt het op een zeker moment zo scheef dat de basis het vloeistofoppervlak
raakt (IIIa). Door het segment steeds lichter te maken, zullen ook de
situaties zoals getekend in (IV), (IIb) en (V) optreden, in die volgorde.

Propositie 10
Gegeven een lichaam in de vorm van een recht segment van een
paraboloïde met as groter dan 15/8p. Als dit segment
in de vloeistof wordt geplaatst met zijn basis geheel boven het oppervlak,
dan:
- Als sgs : sgv < AR2 : AM2 dan is het lichaam
in evenwicht in de positie waarin de as verticaal staat.
- Als Q1Q32 : AM2 < sgs :
sgv < AR2 : AM2 dan is het lichaam niet in
evenwicht als zijn basis het oppervlak van de vloeistof in een punt
raakt, maar in een zodanige positie dat zijn basis de vloeistof nergens
raakt en zijn as met het oppervlak een hoek maakt groter dan U.
- a) Als sgs : sgv = Q1Q32 : AM2
dan is het lichaam in evenwicht in de positie waarin de basis het
oppervlak in een punt raakt en de as met het oppervlak een hoek maakt
gelijk aan de hoek bij U.
b) Als sgs : sgv = P1P32 : AM2
dan is het lichaam in evenwicht wanneer zijn basis het oppervlak van de
vloeistof in een punt raakt en de as met het oppervlak een hoek maakt
gelijk aan de hoek bij T.
- Als P1P32 : AM2 < sgs :
sgv < Q1Q32 : AM2 dan is
het lichaam in evenwicht in een positie waarbij zijn basis gedeeltelijk
ondergedompeld is.
- Als sgs : sgv < P1P32 : AM2
dan is het lichaam in evenwicht in een positie waarin zijn as met het
oppervlak van de vloeistof een hoek maakt kleiner dan de hoek bij T,
maar zo dat de basis het oppervlak nergens raakt.
In boek II in tabel
|
as # ¾p |
rechtop |
|
|
|
as > ¾p |
|
sgs : sgv $ (as - ¾p)2
: as2
rechtop
|
|
¾p < as < 15/8p |
sgs : sgv < (as - ¾p)2 : as2
schuin
|
|
|
|
|
as > 15/8p |
schuin |
raakt |
snijdt |
raakt |
schuin |
rechtop |
Van links naar rechts wordt de verhouding sgs : sgv groter
(Boven elkaar gelegen stippellijnen geven géén verticaal verband aan)
DISCUSSIE:
Je kan je afvragen waarom Archimedes zich hiermee heeft beziggehouden. Een voor
de hand liggend idee is natuurlijk: scheepsbouw. Maar waarom heeft hij dan
paraboloïden onderzocht? Wel wist hij natuurlijk veel van parabolen en
paraboloïden af. Ook valt een paraboloïde door te zagen en er een
"doorsnede met lengte" tussen te zetten, zodat er een langwerpig
lichaam ontstaat wat veel weg heeft van een bootje én vergelijkende
eigenschappen met de paraboloïde bezit. Toch heeft Archimedes dát niet gedaan.
Een ander probleem die dan ontstaat is de massiefheid van de paraboloïden die
hij gebruikt, terwijl een schip juist niet massief is en dus andere
zwaartepunten heeft.
Helaas kunnen we het hem niet meer vragen.
Literatuur
-
T.L. Heath, A History of Greek Mathematics
Oxfort: Clarendon Press, 1965
-
T.L. Heath, The Works of Archimedes
New York: Dover, ca.1961
-
I. Schneider, Archimedes
Darmstadt: Wissenschaftliche Buchgesellschaft, 1979
S.K. Stein, Archimedes - What did he do besides cry eureka?
Washington DC: Mathematical Association of America, 1999
B.L. van der Waerden, Ontwakende Wetenschap:
Egyptische, Babylonische en Griekse wiskunde
Groningen: Noordhoff, 1950
en verder:







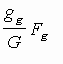 .
.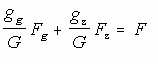 , en dat
is gelijk aan ggFg
+ gzFz = (gg+gz)F,
en dus
, en dat
is gelijk aan ggFg
+ gzFz = (gg+gz)F,
en dus 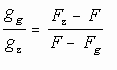 .
.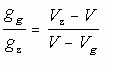 .
Merk op dat deze (natuurlijk) gelijk aan elkaar zijn.
.
Merk op dat deze (natuurlijk) gelijk aan elkaar zijn.









