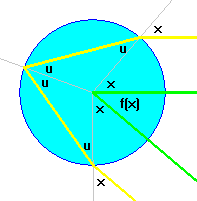
Noem de hoek van inval x en de hoek van uitval u (beide ten opzichte van de normaal). In de tekening is de hoek tussen de in-de-druppel-vallende lichtstraal en de uit-de-druppel-tredende lichtstraal in het groen aangegeven (de benen van de hoek zijn evenwijdig aan de lichtstralen). De grootte van deze hoek wordt weergegeven met de functie f(x).

De hoeken in het middelpunt van de cirkel optellen levert een functievoorschrift voor de hoek op.
![]()
Laat R de brekingsindex van een bepaalde kleur zijn voor de overgang van lucht naar water. Met behulp van de Wet van Snellius kunnen we u uitdrukken in termen van x.
![]()
[arcsin(x) = sin-1(x)]
De combinatie van deze twee levert de vergelijking voor de hoekfunctie f(x).
![]()
Vervolgens afleiden naar x.
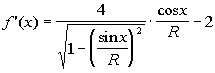
De nu verkregen formule voor de afgeleide kunnen we plotten in een grafische rekenmachine en vervolgens de x-co÷rdinaat van het snijpunt met de x-as (laten) berekenen (zie voorbeeld). Dit nulpunt moet je vervolgens invullen in f(x) om de bijbehorende hoek te krijgen (zie tabel).
Voor de liefhebber toch nog even de tussenstappen zonder grafische rekenmachine:
![]()
En dus:
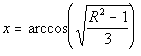
| kleur | R | x (in graden) | f(x)
(in graden) en dus de maximale hoek |
| rood | 1,330 | 59,58 | 42,5 |
| geel | 1,333 | 59,41 | 42,1 |
| blauw | 1,337 | 59,18 | 41,5 |
| violet | 1,341 | 59,95 | 40,9 |
Bij onderstaand voorbeeld is de TI-83 Plus gebruikt.